Manacher算法

[TOC]

简介

Manacher算法，又称🐎拉车算法，是用来求解：

在字符串str中，求出一条最长回文子串，时间复杂度O(n)。

算法解析

方法

中心扩散法+加速

基本概念

统一奇偶长度问题

对于中心扩散法，存在一个问题，就是奇数长度的回文串与偶数长度的回文串求解不统一。

比如：对于'abcbbcbba'，如果我们以每个字符为中心向两边扩散，则会遗失长度为偶数的回文串。(当然我们可以再以相邻字符向两边扩散然后取最大值)

所以我们在字符串中加入辅助字符：

#a#b#c#b#b#c#b#b#a#，然后向两边扩散，得到的长度len除2就是回文串长度。

对于上述字符串我们向两边扩散依次得到：1 3 1 3 1 7 1 3 13 ...所以最长回文子串长度为13/2 = 6，即bcbbcb

回文直径与回文半径数组

• 字符i对应的回文直径为以字符i为中心的回文子串的长度（这里的字符串是加入了辅助字符的

• 回文半径=回文直径/2 + 1

• 定义回文半径数组P

扩散到最右边的回文右边界R

初始int R = -1，从左向右扩散

比如对于：#a#b#c#b#b#c#b#b#a#

第一次从0位置扩散：# 0~0 ==> R=0

第二次从1位置扩散：#a# 0~2 ==> R=2

第三次从2位置扩散：# 2~2 ==> R=2

第四次从3位置扩散：#b# 2~4 ==> R=4

……

取得最远右边界R时的中心位置C

初始int C = -1，从左向右扩散

比如对于：#a#b#c#b#b#c#b#b#a#

第一次从0位置扩散：# 0~0 ==> C=0

第二次从1位置扩散：#a# 0~2 ==> C=1

第三次从2位置扩散：# 2~2 ==> C=2

第四次从3位置扩散：#b# 2~4 ==> C=3

……

算法加速

str = #1#2#1#...，int R = -1，int C = -1

从左向右扩散，记当前位置下标为i

• 1、若i>R，则暴力扩

• 2、若i<=R，做出此时R关于C的对称的L，i关于C的对称点i'，注意这里C与i的为位置关系不确定。

  此时在回文半径数组P中我们可以找到i'的回文半径，所以可以确定i'的回文区域

  • 若[Li,Ri] 是 [L,R]的一个子集，则i的回文长度与i'的回文半径相等（简单的对称性易知

  

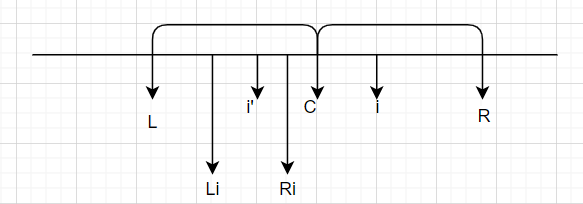
  • 若Li<L，Ri<=R，则i的回文半径为R-i

  

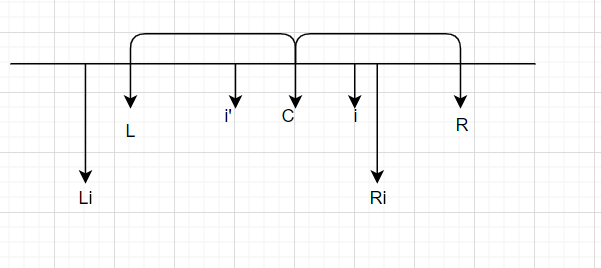
  • 若Li=L，则i的回文半径至少为R-i

原字符串下标与辅助字符串下标对应关系

设原字符串为s：s = abcbd

辅助字符串为str：str = #a#b#c#b#d#

易知：s[i] = str[2i + 1]；即若 s[i] = str[k] ==> k = 2i +1 ==> i = (k - 1)/2 = k/2

伪C++代码：

string str;//处理后的字符串,如：#1#2#1#
int R = -1;
int C = -1;
int P[n];
for(int i = 0; i < str.len; i++){
    if(i > R){
        //从i暴力扩散，更新R,C
    } else {
        if(Li>L){
            P[i] = P[i']; 
        } else if(Li<L) {
            P[i] = R-i;
        } else {
            //从R和2i-R处开始扩散
            //可能更新R,C
        }
    }
}

class Solution {
public:
    void manacherStr(char *str, string &s){
        int k = 0;
        for(int i = 0; i < 2*s.length()+1; i++)
            str[i] = (i & 1) == 0? '#' : s[k++];
    }

    string longestPalindrome(string s) {
        int n = s.length() * 2 + 1; 
        char str[n];
        manacherStr(str, s);
        int p[n]; //回文半径数组
        int C = -1; //中心
        int R = -1; //回文右边界的再往右一个位置，最右有效区是R-1位置
        int maxlen = 1;
        int begin = 0;
        for(int i=0; i < n; i++){
            p[i] = i < R? min(p[2*C-i], R-i) : 1;
            while(i+p[i] < n && i-p[i]>-1){
                if(str[i+p[i]] == str[i-p[i]])
                    p[i]++;
                else
                    break;
            }
            if(i+p[i] > R){
                R = i + p[i];
                C = i;
            }
        }
        for(int i = 0; i < n; i++){
            if(p[i] - 1 > maxlen){ 
                maxlen = p[i] - 1; 
                //由上面的原字符串下标与辅助字符串下标对应关系可以推出
                begin = (i - p[i] + 1)/2;
            }
        }
        return s.substr(begin, maxlen);
    }
};